Sunday, December 5, 2010

While probabilistic approaches to metric mapping have proven highly successful, similar approaches to topological mapping have not yet appeared. Probabilistic Topological Maps (PTMs) offer a general and comprehensive Bayesian solution to the problem of topological mapping. The main thrust is towards solving the perceptual aliasing problem in a manner that supports quantification of the correctness of the mapping result, and hence, graceful failure.
This project aims to extend the probabilistic approach to topological mapping by computing the probability distribution over the space of all topological maps. A probability distribution over topologies, which is a discrete space, looks something like the following (each row is a different distribution)
Probabilistic Topological Maps
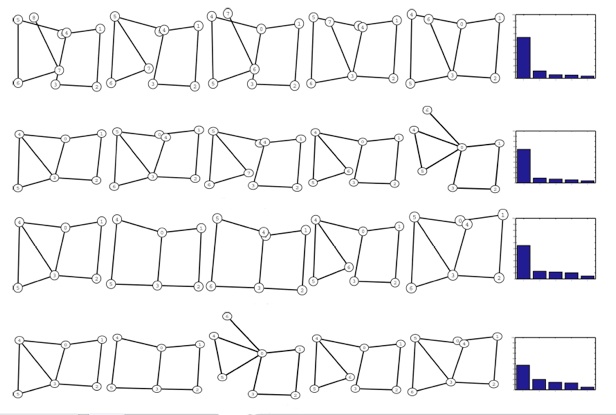
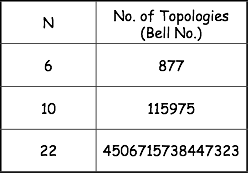
Bayesian inference is used to produce a sample-based representation (as shown above) of the posterior over topological maps using sampling algorithms such as Markov Chain Monte Carlo (MCMC) and Sequential Importance Sampling (SIS). The challenge is to design these algorithms so that they work efficiently and terminate relatively quickly with meaningful results. This is a significant challenge because the number of possible topologies increases at a hyper-exponential rate (faster than exponentially) with the number of landmarks observed. The number of topologies for n landmarks is given by the Bell number. The growth of the Bell number is shown in the table below -
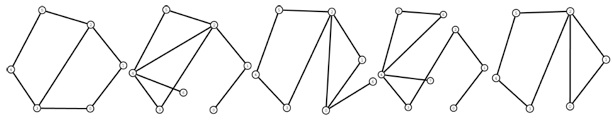
Our computational framework overcomes this challenge of a combinatorial space and also supports the use of a wide variety of sensors (cameras, laser, odometry) that have been used to obtain results presented in the publications listed at the bottom. A couple of environments used in our experiments and their corresponding PTMs are shown below.
The CRB environment layout (right) and the PTM (distribution over topologies) obtained using odometry and visual input (bottom). Topologies are shown in decreasing order of probability from left to right.

PTMs were the topic of my PhD thesis, and Frank and I have built up this edifice over a number of publications.
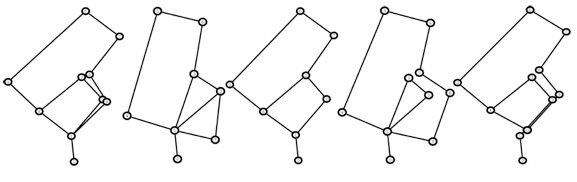
The TSRB environment layout (right) and the PTM (below) obtained using odometry and laser scan data. Topologies are shown in decreasing order of probability from left to right.
Publications
-
•Inference in the Space of Topological Maps: An MCMC-based Approach
Ananth Ranganathan and Frank Dellaert, IROS 2004
This paper introduces the concept of Probabilistic Topological Map (PTM) and provides an algorithm for obtaining a PTM using MCMC sampling. We obtain good results even when using only odometry and no other sensors! -
•Dirichlet Process based Bayesian Partition Models for Robot Topological Mapping
Ananth Ranganathan and Frank Dellaert, GIT-GVU-04-21 2004
In this tech report, we explore the use of the Dirichlet Process as a prior over topologies. The Dirichlet process encodes the intuition that places that have been visited frequently in the past are also more likely to be visited in the future. Results obtained using this prior show a significant improvement over the use of a uniform prior on the space of topologies.
-
•Data driven MCMC for Appearance-based Topological Mapping
Ananth Ranganathan and Frank Dellaert, RSS 2005
This paper extends the previous paper by introducing the use of Fourier signatures of panoramic images as appearance measurements. In addition, we provide a data-driven proposal distribution using odometry that significantly improves the efficiency of the algorithm.
-
•Bayesian Inference in the Space of Topological Maps
Ananth Ranganathan, Emanuele Menegatti, and Frank Dellaert
IEEE Transactions on Robotics, 2006
This journal paper combines the work of the previous two papers and, in addition, introduces the use of an urn-model prior over the space of topologies. This prior encodes a form of Occam's razor by making topologies with a large number of distinct landmarks unlikely. The prior also states that the robot is equally likely to visit any of the landmarks visited previously or a completely new landmark at any point in time.
-
•A Rao-Blackwellized Particle Filter for Topological Mapping
Ananth Ranganathan and Frank Dellaert, ICRA 2006
This paper adds to the previous work by providing a means to compute the PTMs incrementally using particle filtering. While the state space is combinatorial in nature, efficient computation is made possible by Rao-Blackwellization using the location of the landmarks. A data-driven proposal distribution is used for fast convergence. This is also the first PTM paper to use laser range scans as sensor input.
-
Ananth Ranganathan and Frank Dellaert, ICRA 2009.
None of the previous papers deal with the problem of landmark detection, i.e. identifying which places are worthy of becoming nodes in the topological map. In this paper, we propose the use of Bayesian surprise, first used in computer vision, for this purpose. The results, obtained in conjunction with the PTM algorithm, are promising. -
-
Ananth Ranganathan and Frank Dellaert
-
International Journal of Robotics Research, In Press
This paper extends the particle filtering algorithm to use a bag-of-words appearance model founded on the Multivariate Polya distribution. This model is more powerful than the Fourier signatures used previously. We present extensive results on widely used SLAM datasets as well as timing comparisons between the various PTM algorithms.