Real-time Smoothing and Mapping

Smoothing and Mapping (SAM) refers to the framework wherein the SLAM problem is solved using a smoothing approach rather than the commonly used filtering one. The primary computational advantage arises due to the smoothing information matrix that remains sparse without the need for any approximations. SAM is based on QR and Cholesky matrix factorizations that greatly speed up the optimization procedure leading to a very efficient algorithm.
However, the originally proposed SAM algorithm had the disadvantage of being a batch algorithm that had to recompute the solution for all the poses and features at each step. This project has the aim of producing incremental SAM algorithms that run in constant time except in rare cases. To achieve this, we have been following two parallel paths. One technique leverages the linear algebra literature relating to the update of matrix factorizations, while the other view proceeds from a graphical model view of the SLAM problem where we try to perform incremental inference.
The result has been two algorithms - incremental SAM, based on Givens rotations to update the QR factorization of a matrix, and Loopy SAM, based on loopy belief propagation performed in an incremental manner so that the message updates can be done in constant time per step.
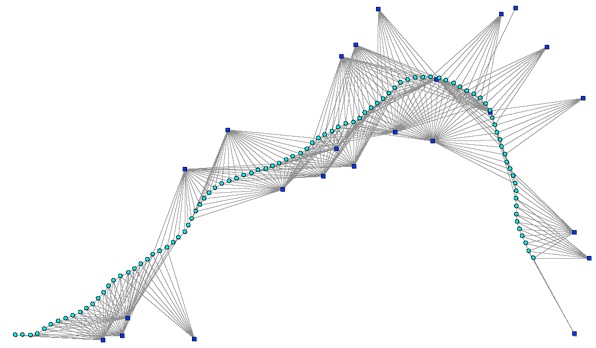
The SAM problem as an MRF
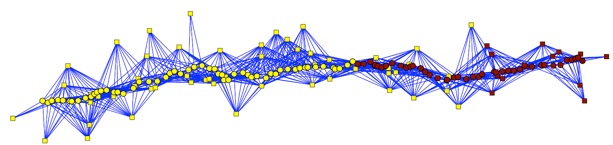
Loopy Belief Propagation on the MRF solves the SAM problem. Only the nodes near the robot (in red) are updated here.
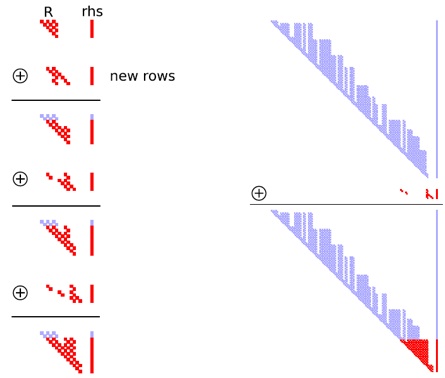
When the factorization of matrix (here the triangular matrix R of a QR factorization) is updated incrementally upon the addition of a few rows to the original matrix, only a small portion of the entries get changed (shown in red).
Publications
-
•Fast Incremental Square Root Smoothing
Michael Kaess, Ananth Ranganathan, and Frank Dellaert, IJCAI 2007.
This paper introduces a matrix factorization approach to SAM by incrementally updating the Cholesky factor of the Hessian matrix for the SLAM problem. New measurements involve the addition of new rows to the Hessian. The Cholesky factor can be updated through incremental QR factorization using Givens rotations. This results in an extremely fast algorithm. -
•Loopy SAM
Ananth Ranganathan, Michael Kaess, and Frank Dellaert, IJCAI 2007.
This paper formulates the SLAM problem as a Markov Random Field (MRF) on which inference is done through loopy belief propagation to obtain the estimates of the robot and landmark locations. We show that when the robot is not closing a loop, each step involves the addition of a few nodes to the MRF. The resulting loopy belief update does not affect the whole MRF graph when messages are thresholded, resulting in a fast algorithm. We also provide a theoretical proof showing the equality between Gauss-Seidel elimination on the MRF matrix and loopy belief propagation on the MRF graph.